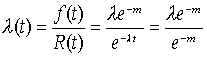|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
1/2 |
|
| |
|
故障・信頼性の手法 |
|
|
|
| |
|
|
|
| |
1. |
故障・信頼性手法の内容 |
|
|
|
| |
|
次の手法について、データを入力することにより、分析をすることが出来る。 |
|
|
|
| |
|
|
|
| |
|
No |
分 析 の 区 分 |
使用分布 |
分 析 内 容 の 説 明 |
|
|
| |
|
1 |
適合度の検定 |
|
指数分布 |
指数分布の適合度 |
|
|
|
|
| |
|
2 |
平均寿命の信頼限界 |
指数分布 |
全部が故障した場合 |
|
|
|
|
| |
|
3 |
平均寿命の信頼限界 |
指数分布 |
一定時間後追跡を中止した場合 |
|
|
|
| |
|
4 |
平均寿命の信頼限界 |
指数分布 |
一定個数で中止した場合 |
|
|
|
|
| |
|
5 |
指数分布の計算 |
指数分布 |
指数分布の一般的な式を使用する場合 |
|
|
|
| |
|
6 |
市場クレーム |
|
ワイブル分布 |
使用経過月データの場合(累積故障法) |
|
|
|
| |
|
7 |
市場クレーム |
|
ワイブル分布 |
走行距離別データの場合(累積故障法) |
|
|
|
| |
|
8 |
市場クレーム |
|
ワイブル分布 |
走行距離別データの場合(メジアンランク法) |
|
|
|
| |
|
9 |
試験データ |
|
ワイブル分布 |
全部が故障の場合(γ変換未反映) |
|
|
|
| |
|
10 |
試験データ |
|
ワイブル分布 |
全部が故障の場合(γ変換反映) |
|
|
|
| |
|
11 |
試験データ |
|
ワイブル分布 |
未故障のある場合(メジアンランク法) |
|
|
|
|
|
|
| |
|
12 |
試験データ |
|
ワイブル分布 |
未故障のある場合(瞬間故障法) |
|
|
|
|
|
|
| |
|
|
(1) |
No.7は市場クレームにも使用可能である。(No.9を使用してγ変換も可) |
|
|
|
|
|
|
| |
|
|
(2) |
ワイブル分布のプロットが直線に回帰する(線にほぼ乗っている)場合は、γ(位置のパラメータ) |
|
|
|
|
|
| |
|
特 |
|
は「ゼロ」としてデータはそのまま入力すればよいが、回帰しない場合はγを適宜決めて |
|
|
|
|
|
| |
|
記 |
|
全てのデータからγ値を減じてデータを入力又はその計算をし直す必要がある。 |
|
|
|
|
|
|
| |
|
事 |
|
No.7にその手法があります。 |
|
|
|
|
|
|
|
| |
|
項 |
(3) |
時間数や距離数などのtの値はLog-Logの計算の都合上、0.1〜100以下になるよう |
|
|
|
|
|
| |
|
|
|
変数変換をしてデータを入力して下さい。 |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
| |
2. |
用語の説明 |
|
|
|
|
|
|
|
|
|
|
| |
|
2.1 |
信頼性の手法 |
|
|
|
|
|
|
|
|
|
|
| |
|
製品やシステムの故障発生率や耐用期間を評価する方法をいう。 |
|
|
|
|
|
|
|
|
| |
|
2.2 |
信頼性 |
|
|
|
|
|
|
|
|
|
|
| |
|
機器、装置、部品などのアイテムが与えられた条件で、規定の期間中、要求された機能を故障しない |
|
|
|
|
|
| |
|
で果たす能力をいい、信頼度はその確率をいう。 |
|
|
|
|
|
|
|
|
|
| |
|
2.3 |
信頼度R(t) |
|
|
|
|
|
|
|
|
|
|
| |
|
|
機器、装置、部品などのアイテムが与えられた条件で、規定の期間中、要求された機能を故障しない |
|
|
|
|
|
| |
|
|
で果たす確率をいい、次のとおり定義をする。 |
|
|
|
|
|
|
|
|
|
| |
|
|
信頼度R(t)+不信頼度F(t)=1⇒F(t)=1-R(t)=1-e-λt |
|
|
|
|
|
|
|
|
|
| |
|
|
|
R(t)は時間的に信頼度が「1」からどのように減じていくのかを示す。 |
|
|
|
|
|
|
|
|
| |
|
|
|
F(t)は「0」から「1」に向かって故障する割合がどのように増大するのかを示している。 |
|
|
|
|
|
|
| |
|
|
この標準でいう時間とは、時間に関係する特性をいい、距離も時間的観念の特性である。 |
|
|
|
|
|
|
| |
|
2.4 |
故障 |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
故障とは、機器、装置、部品などのアイテムが要求された機能を失うことをいう。 |
|
|
|
|
|
|
| |
|
2.5 |
故障率λ(t) |
|
|
|
|
|
|
|
|
|
|
| |
|
故障率λ(t)は、ある時点まで故障しないで作動してきたアイテムが、引き続く単位時間内に故障 |
|
|
|
|
|
|
| |
|
|
を起す割合をいい、次のように定義をする。 |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
f(t):確率密度関数 |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
2/2 |
|
|
|
|
|
| |
|
2.6 |
ワイブル分布 |
|
|
|
|
|
|
|
|
|
|
| |
|
形状のパラメータm、尺度のパラメータη、位置のパラメータγによって定まる分布をいい、実測データを対数 |
|
|
|
|
|
| |
|
目盛りを使用して論理曲線にあてはめたもので、次式で表される。 |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
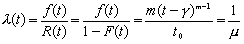
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
2.7 |
指数分布 |
|
|
|
|
|
|
|
|
|
|
| |
|
ワイブル分布の形状のパラメータmが1の時の分布をいい、次式で表される。 |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
2.8 |
各パラメータ |
|
|
|
|
|
|
|
|
|
|
| |
|
(1) |
形状のパラメータm |
|
|
|
|
|
|
|
|
|
|
| |
|
故障モードともいい、分布の形(故障形態)を表す本質的なパラメータである。 |
|
|
|
|
|
|
|
| |
|
(2) |
尺度のパラメータη |
|
|
|
|
|
|
|
|
|
|
| |
|
分布の広がりを示すパラメータである。 |
|
|
|
|
|
|
|
|
|
|
| |
|
(3) |
位置のパラメータγ |
|
|
|
|
|
|
|
|
|
|
| |
|
故障が発生する時期を示し、通常はγ=0とする。 |
|
|
|
|
|
|
|
|
|
| |
|
γ>0の時は製品などの保証時間(その時間までは故障しないこと)を表す。 |
|
|
|
|
|
|
|
| |
|
2.9 |
故障の形態 |
|
|
|
|
|
|
| |
|
(1) |
初期故障 |
|
|
|
|
|
|
| |
|
|
使用開始後の比較的早い時期に設計、製造上の欠陥もしくは使用環境との不適合によって生 |
|
| |
|
|
ずる故障をいいm<0.8の時をいう。(一般的にはm<1.0とされている) |
|
|
|
|
| |
|
(2) |
偶発故障 |
|
|
|
|
|
|
| |
|
|
初期故障期間を過ぎ、摩耗故障期間に至る以前の時期に偶発的に発生する故障をいう。 |
|
|
| |
|
|
m=1の時をいう。 |
|
|
|
|
|
|
| |
|
(3) |
摩耗故障 |
|
|
|
|
|
|
| |
|
疲労、摩耗、老化現象などによって時間とともに故障率が高くなる時期の故障をいい、m>1.3の |
|
| |
|
時をいう。(一般的にはm>1.0とされている) |
|
|
|
|
|
| |
|
2.10 |
メジアンランク法 |
|
|
|
|
|
|
| |
|
|
累積故障率を算出する場合に使用する方法の1つで次式による簡便法を使用した。 |
|
|
|
| |
|
|
n個中i番目のメジアンランク=((i-0.3)/(n+0.4)) |
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
3. |
検定結果の判定 |
|
|
|
|
|
|
| |
|
検定の判定結果は、「**」印、「*」印又は空白で表示する。・・・付図表-1のみ |
|
|
|
| |
|
(1) |
「**」印は、有意水準(=危険率)が2%で有意であることを示し、「高度に有意である」ことになる。 |
|
| |
|
(2) |
「*」印は、有意水準(=危険率)が5%で有意であることを示し、単に「有意である」ことになる。 |
|
|
| |
|
(3) |
「空白」は、「有意差があるとはいえない」ということになる。 |
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|